LeetCode刷题集锦

5. 最长回文子串

题目描述

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2：

输入: "cbbd"
输出: "bb"

解题思路

①想到最优子结构

大字符串是回文，把首尾字符取去掉后小字符串也是回文 aba是回文，取首尾后子串b也是

②最小子问题

只有一个字母，必定是回文

有两个子母且两个字母相等才是回文

③状态转移方程 最小子问题如何推出大问题 $$ dp(i,j)=\begin{cases} true & i==j只有一个字母 \
str[j]==str[i] & j-i==1两个子母 \
dp(i+1,j-1)且str[j]==str[i] &j-i>1 大于两个字母 \end{cases} $$ ④实现动态规划

dp二维数组表示【i，j】范围子串是否为回文，注意遍历的顺序，当大于两个字母时要左下的数组值才能使用状态转移，所以遍历从最后行自左向右遍历

实现代码

func longestPalindrome(s string) string {
    result_s,result_e := 0,0
    length := len(s)
    dp := make([][]bool, length)

  
    for i:=0; i <= length-1; i++ {
        dp[i] = make([]bool, length)
    }

    for i:=length-1;i>=0;i-- {
        for j:=i;j<=length-1;j++ {
            if i==j || (j-i==1 && s[i]==s[j]) || (j-i>1 && dp[i+1][j-1] && s[i]==s[j]){
                dp[i][j] = true
                if(j-i > result_e-result_s) {
                    result_s,result_e = i,j
                }
            }else {
                dp[i][j] = false
            }
        }
    }

    return s[result_s:result_e+1]

}

62. 不同路径

题目描述

点链接

解题思路

①想到最优子结构

到图中某一点的步数取决于其上方和左方两个位置的走法

②最小子问题

在起点，不用走只有一种走法

③状态转移方程 最小子问题如何推出大问题 $$ dp(i,j)=\begin{cases} 1 & i=0||j=0 \
dp(i-1,j)+dp(i,j-1) &j!=0||i!=0>1 \end{cases} $$ ④实现动态规划

实现代码

注：实现代码多用了一行一列省去了对边界条件的判断

func uniquePaths(m int, n int) int {
     dp := make([][]int, m+1)
     for i:=0;i<m+1;i++ {
         dp[i] = make([]int,n+1)
     }
    dp[0][1]=1
    for i:=1;i<m+1;i++{
        for j:=1;j<n+1;j++{
            dp[i][j]=dp[i-1][j]+dp[i][j-1]
        }
    }
    return dp[m][n]

}

63. 不同路径 II

题目描述

点链接

解题思路

①想到最优子结构

到图中某一点的步数取决于其上方和左方两个位置的走法

②最小子问题

在起点，不用走只有一种走法

在障碍物点上，可能的结果为0中

③状态转移方程 最小子问题如何推出大问题 $$ dp(i,j)=\begin{cases} 1 & (i=0||j=0)且obstacleGrid[i][j]==0 \
0 & obstacleGrid[i][j]==1\
对应上一步位置不是障碍物的点dp(i-1,j)+dp(i,j-1) &obstacleGrid[i][j]==0且(i!=0)且j!=0 \end{cases} $$ ④实现动态规划

实现代码

func uniquePathsWithObstacles(obstacleGrid [][]int) int {
    m,n := len(obstacleGrid),len(obstacleGrid[0])
     dp := make([][]int, m)
     for i:=0;i<m;i++ {
         dp[i] = make([]int,n)
     }
     //初始化
     if(obstacleGrid[0][0]==0){
        dp[0][0] = 1
    }
    
     //迭代
     for i:=0;i<m;i++ {
         for j:=0;j<n;j++ {
             if(obstacleGrid[i][j]==1){//该点不可达
                 dp[i][j]=0
             }else {//该点可达
                if(isValiated(i-1,j,m,n)&&obstacleGrid[i-1][j]==0){
                    dp[i][j] += dp[i-1][j]
                }
                if(isValiated(i,j-1,m,n)&&obstacleGrid[i][j-1]==0){
                    dp[i][j]+=dp[i][j-1]
                }
             }
         }
     }

    return dp[m-1][n-1]

}

func isValiated(i, j , m, n int) bool {
    if(i<0 || j<0||i>=m ||j>=n){
        return false
    }
    return true
}

64. 最小路径和

题目描述

解题思路

先想到最优子结构，到某一点路径和最小其实就是到上、左两侧点最小路径和 中的最小值+本点的值

然后想最小子问题

然后想状态转移方程，如何大问题如何化为更小的问题

最后代码实现 可以自底向上迭代 也可自顶向下递归 +备忘录

实现代码

class Solution {
    public int minPathSum(int[][] grid) {
        if (grid == null || grid.length < 1 || grid[0] == null || grid[0].length < 1) {
            return 0;
        }
        
        int row = grid.length;
        int col = grid[row - 1].length;
        
        int dp[][] = new int[row][col];
        
        dp[0][0] = grid[0][0];
        
        for (int i = 1;i < row;i++) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        
        for (int i = 1;i < col;i++) {
            dp[0][i] = dp[0][i - 1] + grid[0][i];
        }
        
        for (int i = 1;i < row;i++) {
            for (int j = 1;j < col;j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        
        return dp[row - 1][col - 1];
    }
}

91. 解码方法

题目描述

解题思路

求最优子结构：长的字符的编码可能等于 删去一个字符、删去两个字符的可能之和

最小子问题：只有一个字符时 为0 没有可能 不为0 有1中可能

状态转移方程： $$ dp(i)=\begin{cases} 1 & i==0||i==1\
dp[i-1]+dp[i-2] &i>1 \end{cases} \备注：dp[i-1]条件：str[i]!=‘0’;dp[i-2]条件：str[i]==‘1’||(str[i]==2&&‘0’<=str[i-1]<=‘6’) $$

实现代码

func numDecodings(s string) int {
    if(s[0] == '0') {
        return 0
    }
    dp := make([]int, len(s)+1)
    dp[0],dp[1] = 1,1 //0是为了当只有两个字符时如果删去两个字符dp[0]表示算为有一种可能

    for i:=2; i<len(s)+1; i++ {

        if(s[i-1]!='0'){
            dp[i] = dp[i] + dp[i-1]
        }
        if(s[i-2]=='1'||(s[i-2]=='2' && s[i-1]<='6' && s[i-1]>='0')) {
                dp[i] = dp[i]+dp[i-2]
        }

    }
    return dp[len(s)]
}

难点备注

当只有两个数字时对于dp[i-2]会出现越界的情况，所以dp数组比字符串长度多一位，用最后一位为1表示当两个数字可以解码成字母时会+1

120. 三角形最小路径和

解题思路：

最优子结构 最小子问题 状态转移方程 迭代+dp数组代码实现

实现代码

func minimumTotal(triangle [][]int) int {
    if(triangle==nil) {
        return 0
    }
    width,length := len(triangle),len(triangle) 
    dp  := make([][]int, width)
    for i:=0;i<width;i++ {
        dp[i] = make([]int, length)
    }

    dp[0][0] = triangle[0][0]
    for i:=1; i<width;i++{
        for j:=0; j<=i;j++{
            dp[i][j] = 100000
            if(j-1>=0) {
                dp[i][j] = dp[i-1][j-1] +triangle[i][j]
            }
             if(j <= i-1 &&dp[i][j] > dp[i-1][j] + triangle[i][j]) {
                dp[i][j] = dp[i-1][j] + triangle[i][j]
            }
        }
    }
    min := dp[width-1][0]
    for i:=1;i<length;i++ {
        if(min > dp[width-1][i]) {
            min = dp[width-1][i]
        }
    }
    return min
}

空间压缩优化

dp[i][j]=min(dp[i-1][j-1], dp[i-1][j])本层和上面一整层有关系，而一层最多有n各个元素，所以空间可压缩到O(n)

所以先想到两个一维数组的方法

func minimumTotal(triangle [][]int) int {
    if(triangle==nil) {
        return 0
    }
    length := len(triangle)
    if(length == 1) {
        return triangle[0][0]
    }
    dp  := make([][]int, 2) // 压缩空间
    dp[0] = make([]int, length)
    dp[1] = make([]int, length)

    dp[0][0] = triangle[0][0]
    for i:=1; i<length;i++{
        for j:=0; j<=i;j++{
            min := 100000
            if(j-1>=0) {
                min =  dp[0][j-1]+triangle[i][j]
            }
             if(j <= i-1 &&min > dp[0][j] + triangle[i][j]) {
                min = dp[0][j] + triangle[i][j]
            }
            dp[1][j] = min
        }
        for k:=0;k<length;k++{
            dp[0][k] = dp[1][k]
        }

    }
    min := dp[1][0]
    for i:=1;i<length;i++ {
        if(min > dp[1][i]) {
            min =dp[1][i]
        }
    }
    return min
}

继续优化

使用奇数偶数可以省去循环中dp[1][]导入到dp[0][]

进一步优化的话是第二层循环j的那一层使用倒着遍历方法，只用一个数组就行可以避免dp[j]用到dp[j] 、dp[j-1]正向遍历

dp[1]改了dp[1],但是dp[2]还要用dp[1] 如果倒着遍历则可以不影响了。可见逆向思维

309. 最佳买卖股票时机含冷冻期

解题思路：

①找最优子结构:

这个题不太好找， 自变量、因变量的确定

首先是变量种类多:天数、最大利益、好几种不同的选择

这个时候我们不能一眼看出最优子结构，不想走到某地的走法数，有明显的递推关系

第n天的最大利益取决于前面一系列的选择，且第n天取最大利益和第1天取最大利益可能不一样

一方面当我们定了一个自变量和因变量(状态)时，要进行验证是否合适(如何判断合不合适？)

另一方面当一眼看不出来后就不能靠猜的了，此时第一步先把所有选择对应的转换情况写出如下:

第n天可能的情况，则第n+1天的可能情况

通过图我们知道什么因变量(状态)彼此相关可以递推呢?一天的三种状态,到下一天的转换

这个和我们的最大利益值有关系吗？知道第1天三种状态的利益，那第二天三种状态的利益自然也可以知道,对于第二天的卖的状态，是由第一天卖第一天持有股票什么也不做得到的，那 我们只保留最大的利益

这样每一天的三种状态的最大利益就可以递推了

这样依次推到第n天的利益

所以状态自变量定义为三种状态的最大利益 因变量为天数

总结：最优子结构为如果今天卖股票 最大利益 等于 昨天买入股票最大利益和昨天什么不做持有股票的最大利益 两者最大值

②最小子问题，

第一天 没有股票不在冷冻期：0 有股票不在冷冻期:0(这个不存在,递推第二天是要忽略的) 没有股票但在冷冻期:0 (这个是不存在的在第一天,递推第二天时要忽略掉)

为了递推时要对第一天特殊处理，所以把第二天直接写出来

第二天 没有股票不在冷冻期：0 有股票不在冷冻期：max(-prices[0],-price[1]) 没有股票但在冷冻期:price[1]-price[0]

③递推公式

$$ 没有股票不在冷冻期:dp[0][n]=max(dp[0][n-1],dp[2][n-1]) \
有股票不在冷冻期:dp[1][n]=max(dp[0][n-1]-prices[i]，dp[1][n-1]) \
没有股票但在冷冻期:dp[2][n]=max(dp[1][n]+prices[i])

\备注:当n大于1时才执行递推，否则就按最小子问题处理 $$

在画图基础上定下自变量和因变量和我们猜的,如天数、最大利益（无法递推）； 天数+每天做的选择、最大利益(没有递推关系)，这个最大利益做为因变量怎么都无法递推，因为最大利益和每一天的选择都有关系

代码编写

func maxProfit(prices []int) int {
    if prices==nil||len(prices)==0||len(prices)==1{
        return 0
    }

    dp := make([][]int, 3)
    for i:=0;i<3;i++ {
        dp[i] = make([]int, len(prices))
    }
    
    dp[0][1] = 0
    dp[1][1] = max(-prices[1],-prices[0])
    dp[2][1] = prices[1]-prices[0]
    for i:=2;i<len(prices);i++ {
        dp[0][i] = max(dp[0][i-1],dp[2][i-1])
        dp[1][i]=max(dp[0][i-1] - prices[i],dp[1][i-1])
        dp[2][i]=dp[1][i-1]+prices[i]
    }
    return max(dp[0][len(prices)-1], dp[2][len(prices)-1])
}
func max (a,b int) int {
    if a>b {
        return a
    }else{
        return b
    }
}

122. 买卖股票的最佳时机 II

解题思路

每天有两种状态 可买、可卖

实现代码

func maxProfit(prices []int) int {
    if(prices == nil || len(prices)==0) {
        return 0
    }
    dp := make([][]int,2)
    dp[0] = make([]int, len(prices))
    dp[1] = make([]int, len(prices))
    dp[0][0],dp[1][0] = 0, 0-prices[0]
    for i:=1;i<len(prices);i++ {
        dp[0][i] = max(dp[0][i-1], dp[1][i-1]+prices[i])
        dp[1][i] = max(dp[1][i-1], dp[0][i-1]-prices[i])
    }
    return dp[0][len(prices)-1]

}

func max(a,b int) int{
    if a>b{
        return a
    }
    return b
}

121. 买卖股票的最佳时机

解题思路

每日有三个状态 没买过可以买股票、买过但还没有卖、买过而且也卖了 彼此之间转化递推，

如果当天某一状态要去最大利益，取决于昨天可以变为该状态的最大利益加上相应操作带来的影响

实现代码

    func maxProfit(prices []int) int {
        if(prices==nil || len(prices)==0) {
            return 0
        }
        length := len(prices) 
        dp := make([][]int, 3)
        for i:=0;i<3;i++{
            dp[i]=make([]int, length)
        }
        dp[0][0],dp[1][0],dp[2][0] = 0,0-prices[0],0
        for i:=1;i<length;i++ {
            dp[0][i] = 0
            dp[1][i] = max(dp[1][i-1], dp[0][i-1]-prices[i])
            dp[2][i] = max(dp[2][i-1], dp[1][i-1]+prices[i])
        }
        return dp[2][length-1]
    }

    func max(a, b int)  int{
        if(a>b) {
            return a
        }
        return b
    }

322. 零钱兑换

解题思路

凑大钱由凑小钱转移而来 ，有1、2、5三种硬币， 凑11元钱 最少 肯定是 凑11-1 11-2 11-5三种情况中最少硬币数+1

如果三种都没办法凑，那11块钱也没办法凑

最小子问题 dp[0] = 0

$$ dp[i]=min\begin{cases} dp[i-coin[1]] & i-coin[1]>=0\ ……\
dp[i-coin[2]] & i-coin[2]>=0 \end{cases}+1\或者当没有i-coin>=0时dp[i]为-1,凑不成 $$

实现代码

func coinChange(coins []int, amount int) int {
    dp := make([]int, amount+1)
    dp[0] = 0
    for i:=1;i<=amount;i++ {
        min := 10000 //表示不可达
        for _, j := range coins {
            if(i-j >= 0 && dp[i-j]!=-1 &&dp[i-j]<min) {
                min = dp[i-j]
            }
        }
        //如果仍是最大值  表示没有可达
        if min == 10000 {
            dp[i] = -1
        }else {
            dp[i] = min+1
        }
    }
    return dp[amount]
}

198. 打家劫舍

解题思路

不能连续偷东西， 每一间房子有两种状态 (可以偷不会触发警报 、 不可以偷会触发警报)

每经过一间房子都会有什么也不做、偷东西两种动作

最小问题 只有一间房子

dp[0][0] = 0 //第1间可以偷不会触发警报

状态转移方程

dp[1][0] = nums[0] //第1间 不可以偷会触发警报 $$ dp[0][i] = \begin{cases} max(dp[1][i-1],dp[0][i-1]) & i-1房 什么也不做，i-1偷过东西\end{cases} \

dp[1][i] = \begin{cases} dp[0][i-1]+nums[i] &i-1房 可以偷 \end{cases} $$

实现代码

  func rob(nums []int) int {
        if(nums==nil ||len(nums)==0){
            return 0
        }
        length := len(nums)
        dp:=make([][]int, 2)
        dp[0] =make([]int, length)
        dp[1] =make([]int,length)
        dp[0][0],dp[1][0] = 0,nums[0]
        for i:=1;i<length;i++ {
            dp[0][i]=max(dp[0][i-1],dp[1][i-1])
            dp[1][i]=dp[0][i-1]+nums[i]
        }
        return max(dp[0][length-1],dp[1][length-1])
    }
    func max(a, b int) int {
        if a>b{
            return a
        }
        return b
    }

343. 整数拆分

解题思路

这道题怎么说，不是多阶段决策达到最优解这一类型，而是大问题化小问题的分治法问题

大数N的拆分的最大乘机 如果只拆成两个数 有 1,n-1 2,n-2 3,n-3 …… [n/2-1,n/2] 奇数偶数情况不一致

拆成两个数后又可再拆，那就是子问题，如2，n-2 n-2的拆分方式一定是最大乘积

所以大数N的拆分用到了子问题拆分情况

但是注意一点 大数N 拆成2,N-2 后 N-2可以继续拆也可以不拆 这是两种情况

对于 N-2,2 拆不拆2

对于2,N-2拆不拆N-2

总结

最小子问题是n=0 n=1是最大乘积为0（不可以拆分成两个正整数） n=2时 最大乘积为1

之后对于n>2，大数N拆成两个数的所有情况 如2,N -2 可以①N-2不拆，2*N-2 ②N-2拆 子问题拆(N-2)*2

所以状态转移方程为

$$ 状态转移方程 \
dp[n] = \begin{cases} max \big[ i*(n-i),i*dp[n-i]) \big] && n >2 \end{cases} \备注i从1遍历到n-1 $$

实现代码

func integerBreak(n int) int {
    dp := make([]int, n+1)
    dp[0], dp[1], dp[2] = 0, 0, 1
    for i:=3;i<=n;i++ {
        tmp_max := 0
        for j:=1;j<i;j++ {
            no_chai,chai :=j*(i-j),j*dp[i-j]
            tmp_max = max(no_chai, chai, tmp_max)
        }
        dp[i] = tmp_max
    }
    return dp[n]
}

//三个数求最大
func max(x,y,z int) int {
    max := x
    if y>max {
        max =y
    }
    if z>max {
        max =z
    }
    return max 
}

分析问题：对于不是分阶段决策的问题，而是分治法大问题套用小问题的解这种情况，要先写出递归解法，把规律找到

如本题 拆分大问题 只拆成两个数i,n-i 、 继续拆n-i 两种情况最大值 继续拆n-i可以递归调用

我们将原问题抽象为 f(n) 那么 f(n) 等价于 max(1 * f(n - 1), 2 * f(n - 2), …, (n - 1) * f(1)) + 只拆分成两个数1*n-1 2*n-2 ……的情况。

152. 乘积最大子数组

解题思路

暴力解决就是遍历所有i,j的组合可能

这道题还是要向分治方法求解问题，找出大小问题之间的关联

以i为结尾连续子数组的最大乘积，和以i-1结尾的最大乘积之间的关系

可以用以i-1结尾的最大乘积*nums[i],也可以不用前i-1个元素只用nums[i]

备注：这是如何想出来的？连乘关系，nums[i]可能为正负，前面的连乘可能为正负，我们的nums[i]可以并入前面或者不并入前面，

这里很容易忽略第三种情况即 以i-1为结尾的最小乘积*nums[i]负负得正变成了最大，综上 以i为结尾的最大乘积的设为dp[0][i],以i为结尾的最小乘积设为dp[1][i],有三种可能得到

①dp[0][i-1]*nums[i]

②dp[1][i-1]*nums[i]

③nums[i]

对于dp[1][i-1]也是从上面的三种可能得到

最小子问题： dp[0]][0]=nums[i] dp[1][0]=nums[i]

状态转移方程 $$ dp[0][i]=MAX\big[ (dp[0][i-1]*nums[i]), (dp[1][i-1]*nums[i], nums[i]) \big]\
dp[0][i]=MIN\big[ (dp[0][i-1]*nums[i]), (dp[1][i-1]*nums[i]), nums[i] \big] \从两种情况中取最大值、最小值 $$

实现代码

func maxProduct(nums []int) int {
    dp := make([][]int, 2)
    dp[0] = make([]int, len(nums))
    dp[1] = make([]int, len(nums))
    dp[0][0], dp[1][0] = nums[0], nums[0]
    for i:=1; i < len(nums);i++ {
        dp[0][i] = Max(dp[0][i-1]*nums[i], dp[1][i-1]*nums[i], nums[i])
        dp[1][i] = Min(dp[0][i-1]*nums[i], dp[1][i-1]*nums[i], nums[i])
    }
    max := -100000
    for _,i:=range dp[0] {
        if max < i {
            max = i
        }
    }
    return max
}

func Max(x, y, z int) int {
    max := x
    if y>max {
        max =y
    }

    if z>max {
        max =z
    }
    return max
}

func Min(x, y, z int) int {
    min := x
    if y<min {
        min =y
    }

    if z<min {
        min =z
    }
    return min
}

300. 最长上升子序列

解题思路

自变量：考虑到第i个数字

状态考虑:

①前i个数最长上升子序列的长度

状态之间没有关联，知道前i的最长，但是前i+1的也没有足够的 信息推出来——因为我们不知道前i最长是那几个数，第i+1的数又是否可以接上去

②以第i个数结尾的最长上升子序列长度

知道前i个数结尾的最长长度，可以判断第i+1个数是否可以接到后面,

第i+1个数比后面i个数大则可以接上，总可以接上的所有可能中选出最长的情况

最小子问题:dp[0]=1 只有一个数字

转载leetcode的图https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/tu-jie-zui-chang-shang-sheng-zi-xu-lie-by-cheng-xu/

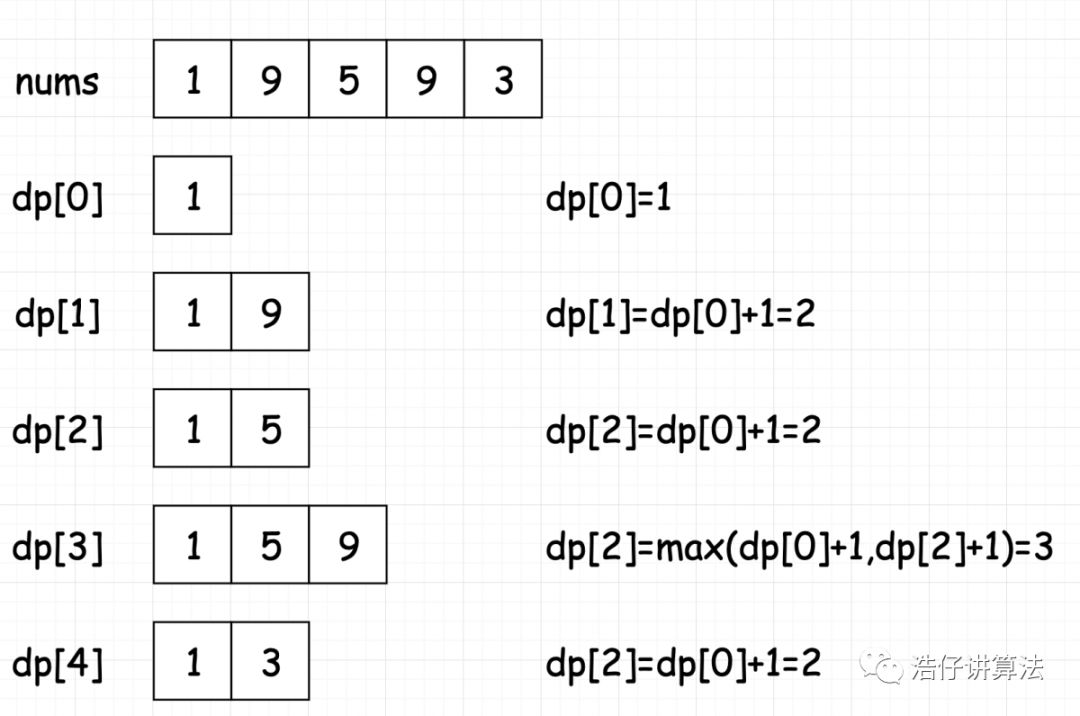
$$ 状态转移方程\
dp[i]=\begin{cases} MAX \bigg(dp[j]+1\bigg) &j从0到i-1,且nums[i]>nums[j] \end{cases} \
如果nums[i]比前面的nums[j]都大则dp[i]=1 $$

实现代码

func lengthOfLIS(nums []int) int {
    if len(nums)==0 {
        return 0
    }
    result := 1
    dp := make([]int, len(nums))
    dp[0] = 1
    for i:=1;i<len(nums);i++ {
        max := 1
        for j:=0; j<i; j++{
            if dp[j]+1 > max && nums[i] >  nums[j] {
                max = dp[j]+1
            }
        }
        dp[i] = max
        if result < dp[i] {
            result = dp[i]
        }
    }
    return result
    
}

复杂度为O(n2),空间复杂度O(n)

进一步优化

将复杂度变为O(nlogn)

思路：贪心算法+二分查找

贪心算法要每次做的选择得到最优解，连续做的最优选择就时最后的解

我们每次做的最有选择就是 尽可能的缩短我们上升子序列的最大值

当nums[i+1] > nums[i],可以放入一个数据

当nums[i+1] <=nums[i] 将其替换第一个小于nums[i]的数，这样我们可以尽可能的多放进

354. 俄罗斯套娃信封问题

将其按w递增排序，同样的h按递减排序就变成了最长上升子序列问题

实现代码

import (
	"fmt"
	"sort"
)
func maxEnvelopes(envelopes [][]int) int {
    sort.Slice(envelopes, func (i, j int)bool {
		if envelopes[i][0]==envelopes[j][0]{
			return envelopes[i][1] > envelopes[j][1]
		}
		return envelopes[i][0] < envelopes[j][0]
    })
    return maxLength(envelopes[:][1])

}

//最长上升子序列
func maxLength(nums []int) int{ 
    length := len(nums)
    if length == 0 {
        return 0
    }
    dp := make([]int ,length)
    dp[0] = 1
    for i:=1;i<length;i++ {
        dp[i] = 1
        for j:=0;j<i;j++ {
            if nums[i]>nums[j] && dp[i] < dp[j]+1 {
                dp[i] = dp[j]+1
            }
        }
    
    }
    max := dp[0]
    for k:=0;k<length;k++ {
        if max < dp[k] {
            max = dp[k]
        }
    }
    return max
}

引申

对于三维的嵌套问题，则要去引入树状数组这一结构来解决问题，问题更复杂

213. 打家劫舍 II

解题思路

和打家劫舍很像，只是第1和第n间房有冲突关系

我们可以假设两种情况

第一间偷，第2不可偷 第3~第n-1间房用动态规划求得最大价值

第一间不偷，第2~第n间房用动态规划求得最大价值

动态规划问题就是不能连续偷的情况下可获得的最大价值

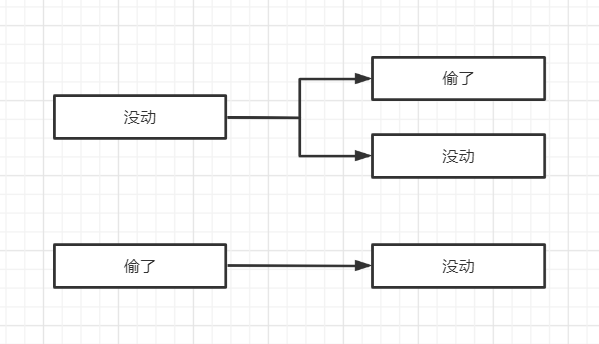
每一间房有两个状态dp[0]没动，dp[1]偷了 $$ 没动dp[0][i]= max\bigg(dp[0][i-1]+nums[i],dp[1][i-1]\bigg)

\
偷了dp[i][i-1]=dp[0][i-1] $$ 对于第一天偷第二天不偷，从第三天开始算

第三天 没动状态 dp[1][2] 为nums[0]

第三天 偷了状态 不存在 dp[1][2] 特别小到第四天直接舍去 (因为第二天没有偷)

对于第一天不偷，从第二天开始算

第二天没动 dp[0][1]=0

第二天偷了状态 dp[1][1]=nums[1]

实现代码

代码不是很好，优化方案:对于动态规划重复逻辑进行复用

func rob(nums []int) int {
    length := len(nums)
    if length==0 {
        return 0
    }
    if length==1 {
        return nums[0]
    }

    dp := make([][]int, 2)
    dp[0], dp[1] = make([]int, length), make([]int, length)
    dp[0][0], dp[1][0],dp[0][1], dp[1][1] = nums[0], 0, nums[0], 0 //第一天偷了,第二天没偷
    for i:=2;i<length-1;i++ {
        dp[0][i] = max(dp[0][i-1], dp[1][i-1])
        dp[1][i] = dp[0][i-1] + nums[i]
    }
    maxVal := max(dp[0][length-2], dp[1][length-2])
    // 重置为0
    for i:=0;i<length;i++ {
        dp[0][i], dp[1][i] = 0, 0
    }
    dp[0][0], dp[1][0] = 0, 0 // 第一天没投
    for i:=1;i<length;i++ {
        dp[0][i] = max(dp[0][i-1], dp[1][i-1])
        dp[1][i] = dp[0][i-1] + nums[i]
        
    }
    maxVal2 := max(dp[0][length-1], dp[1][length-1])

    return max(maxVal, maxVal2)
    
}

func max(a, b int) int {
    if a>b {
        return a
    }
    return b
}

优化代码如下

func rob(nums []int) int {
    length := len(nums)
    if length==0 {
        return 0
    }
    if length==1 {
        return nums[0]
    }
    if length<=3 { // 对于长度为2的nums[2:length-1]会 出现越界异常   长度为3则是nums[2:length-1]会把第三房偷的情况也返回
        return max(nums[0],  MyRob(nums[1:length]))
    }
    return max(MyRob(nums[2:length-1])+nums[0], MyRob(nums[1:length]))
    
}

func MyRob(nums[] int) int{
    length := len(nums)
    if length==0 {
        return 0
    }
    if length==1 {
        return nums[0]
    }
    dp := make([][]int, 2)
    dp[0],dp[1] = make([]int ,length), make([]int, length)

    dp[0][0], dp[1][0] = 0, nums[0]
    for i:=1;i<length;i++ {
        dp[0][i] = max(dp[0][i-1], dp[1][i-1])
        dp[1][i] = dp[0][i-1] + nums[i]
        
    }
    return  max(dp[0][length-1], dp[1][length-1])

}

func max(a, b int) int {
    if a>b {
        return a
    }
    return b
}

也可以是思路

在不偷窃第一个房子的情况下（即 nums[1:]nums[1:]），最大金额是 p1

在不偷窃最后一个房子的情况下（即 nums[:n-1]nums[:n−1]），最大金额是 p2 综合偷窃最大金额： 为以上两种情况的较大值，即 max(p1,p2)

作者：jyd 链接：https://leetcode-cn.com/problems/house-robber-ii/solution/213-da-jia-jie-she-iidong-tai-gui-hua-jie-gou-hua-/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

337. 打家劫舍 III

解题思路：

树状dp问题，第一次遇见啊。

每一个节点定义两种状态，已偷和没动

状态转移如下：

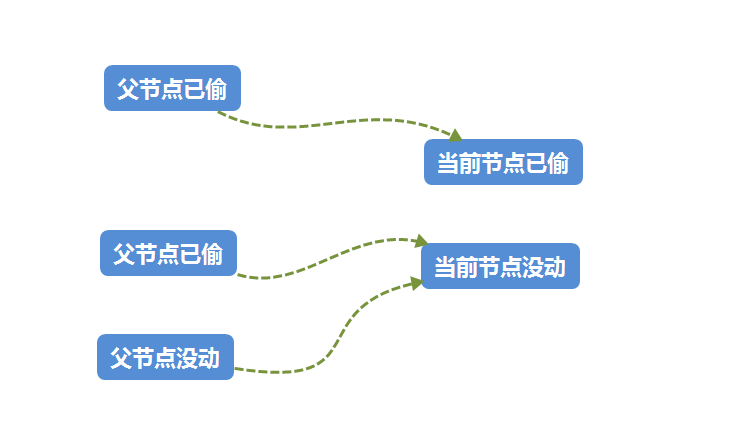
当前节点没动和已偷两种状态下各自可获得的最大价值

自变量是每一个节点，因变量是遍历顺序可以获取最大的价值

难点是原来是数组状态转移方程就是数组dp[i],但是现在是二叉树。

先看状态转移方程 $$ 没动dp[i][0] = 所有子节点\sum max(dp[i-1][0],dp[i-1][1]) 当父节点没动子节点可偷可不偷 \
已偷dp[i][1]=所有子节点\sum dp[i-1][0] +nums[i]当父节点已偷子节点都不能偷 $$ 父节点可以获取的两种状态价值取决于子节点，要先知两个子节点再求父节点—–后续遍历

//伪代码
递归函数func(入参节点node) (返回  do已偷状态价值， undo没动状态价值) {
	if node ==null { 
		//节点为空，两个返回0
    }
    
    leftDo, leftUndo =  func(左节点)的已偷 没动可获价值
    rightDo, rightUndo =  func(右节点)的已偷 没动可获价值
    
	//当前节点已偷=子节点没有偷的情况+当前节点的价值
    curDo = leftUndo + rightDo + nums[cur] 
    //当前节点没动=子节点偷或不偷两种状态可获价值最大值
    curUndo = max(leftDo, leftUndo)+max(rightDo, rightUndo)  
}

这样我们可以获取到根节点的两种状态的最大价值，取个最大值即可

实现代码

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func rob(root *TreeNode) int {
    return max(doRob(root))
}

func doRob(node *TreeNode) (int, int) {
    if node == nil {
        return 0, 0
    }
    lundo, ldo := doRob(node.Left)
    rundo, rdo := doRob(node.Right)    
    return  max(lundo, ldo) + max(rundo, rdo), lundo+rundo+node.Val
}

func max(a,b int) int {
    if a>b {
        return a
    }
    return b
}

375. 猜数字大小 II

解题思路

MiniMAX—最小化对方最大收益的问题，比如下棋如何下会使对方的收益最小，博弈树

我们的任务是猜数，那无疑会有好多种情况， 我们猜的顺序和对方选择的数都是不同的组合 问题求的是我们最多花多少钱稳赢

这里给一下其他人的解释：原链接https://www.cnblogs.com/fayin/p/10407176.html

题目下方给出了几个提示：

• 游戏的最佳策略是减少最大损失，这引出了 Minimax 算法，见这里，和这里
• 使用较小的数开始（例如3），看看在最差的情况下你要支付多少钱？
• 即使 n 比较小，完全使用递归的效率也很低，试试动态规划吧。

我们就按照上面的提示玩一把：猜数字大小 II。

当 n = 3，那么我们有 3 个选择：1 或 2 或 3。

假设我们先猜 1，就有两种情况：

• [猜对]：1 就是正确的数字，所以你支付 0¥，或者
• [猜错]：1 不是正确数字，于是你需要支付 1¥（现在，你知道那个正确的数字 > 1，因为每次猜完后你都将被告知猜大了还是猜小了。但就目前的情况来看正确的那个数肯定比 1 大），于是我们得到了一个子问题（2，3）——在[2,3]范围内猜出正确的数字。运用递归，我们可以使用同样的方法解决这个问题，此时你可以选择 2 或 3。如果选择 2，你又有两个可能的结果：2 是正确的数字于是你支付 0¥，或者 2 不是正确的数字那么你支付 2¥ ，现在你知道正确的数字是 3 了（因为只剩下 3 这个数字）。如果选择 3，要么 3 就是正解要么你支付 3¥ 于是你知道 2 才是正确的答案。总结一下，选择 2 最多支付 2¥，选择 3 最多支付 3¥。两相比较，在支付最多的情况下，我们选择那个最小的值（2¥），即数字 2 作为子问题（2，3）的答案。（注意到 minimax 了么~~）所以，最终的花费是 1¥ + 2¥ = 3¥

如果你最先猜的是 2，同样会有两个可能的结果：

• 2 是正确的数字，你支付 0¥
• 2 不是正确的数字，你支付 2¥。此时，你会知道你猜大还是猜小了，于是你马上就知道哪个才是正确答案了。所以，如果你最先猜 2，你最多支付 2¥。

同样的，如果你最先猜 3，那么你最多需要花费 4¥。

所以，最先猜 2 才是最优选择，你最多花费 2¥。

参考下面的代码，你会看到这是一个十分自然的递归过程。（使用了二维矩阵缓存结果）

public class Solution {
  private int[][]dp;

  private int solve(int l, int r) {
    if (l >= r) return 0;
    // 说明 dp[l][r] 已经被计算过了，直接返回
    if (dp[l][r] != Integer.MAX_VALUE) return dp[l][r];

    for (int i = l; i <= r; ++i) {
      dp[l][r] = Math.min(dp[l][r], Math.max(i + solve(l, i-1), i + solve(i+1, r)));
    }

    return dp[l][r];
  }

  public int getMoneyAmount(int n) {
    dp = new int[n+1][n+1];
    for (int[] row : dp)
      Arrays.fill(row, Integer.MAX_VALUE);

    return solve(1, n);
  }
}

我整理一下: 最优解结构—-区间[i,j]中的稳赢金额 等于
猜i,j中的一个数x后再去猜区间[i,x-1]或者区间[x+1,j] 这会花去 x+MAX(【i,x-1】稳赢金额，【x+1,j】稳赢金额)

遍历所有的x情况中,取最小值 即可得到答案

转移方程 $$ dp[i][j]=\begin{cases} 0 & i =j\
MIN \big[x+ MAX(dp[i,x-1], dp[x+1,j])\big] & i<j至少2个数 \end{cases} \其中x属于[i,j]中的所有情况 $$

举例: 只有两个数

dp[0][1]=MIN(arr[0]+ dp[1][1], arr[1]+dp[0][0])

dp[0][2]

在这里附上go的递推迭代版本,没有经过优化，而且可读性不如递归调用

实现代码

func getMoneyAmount(n int) int {
    dp := make([][]int, n)
    for i:=0; i<n; i++ {
        dp[i] = make([]int, n)
    }
    // 除去了i==j为0，其他都指为100000标识代价很大
    for i:=0; i<n; i++ {
        for j:=0; j<n; j++ {
            if(i!=j){
                dp[i][j] = 100000
            }
        }
    }

    for step:=1; step<n;step++ {
        for start:=0;start<n;start++ {
            if(start+step<n) {
                //推出区间为 start 到  start+dp的 稳赢金额,需要遍历区间内每一种情况
                // 因为x现在是下标,当x=0时实际上花费1
                for x:= start; x<=start+step; x++{
                    if(x-1<0) {
                        dp[start][start+step] = min(dp[start][start+step], x+1+ dp[x+1][start+step])
                    }else if(x+1>=n) {
                        dp[start][start+step] = min(dp[start][start+step], x+1+dp[start][x-1])
                    }else{
                        dp[start][start+step] = min(dp[start][start+step], x+1+max(dp[start][x-1], dp[x+1][start+step]))
                    }
                }
            }else{
                break
            }
        }
    }

    return dp[0][n-1]
}

func max(a, b int) int{
    if a<b {
        a=b
    }
    return a
}
func min(a, b int) int{
    if a>b {
        a=b
    }
    return a
}

附：leetcode java代码

public class Solution {
    public int getMoneyAmount(int n) {
        int[][] dp = new int[n + 1][n + 1];
        for (int len = 2; len <= n; len++) {
            for (int start = 1; start <= n - len + 1; start++) {
                int minres = Integer.MAX_VALUE;
                for (int piv = start; piv < start + len - 1; piv++) {
                    int res = piv + Math.max(dp[start][piv - 1], dp[piv + 1][start + len - 1]);
                    minres = Math.min(res, minres);
                }
                dp[start][start + len - 1] = minres;
            }
        }
        return dp[1][n];
    }
}
复杂度分析

作者：LeetCode
链接：https://leetcode-cn.com/problems/guess-number-higher-or-lower-ii/solution/cai-shu-zi-da-xiao-ii-by-leetcode/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

376. 摆动序列

解题思路

最长上升子序列是定义成以第i个数字结尾的最长上升子序列长度

1 3 2 4

长度依次为 1、2、2、3 dp[i+1]= i+1之前的所有满足arr[i+1]>arr[x]的情况dp[x]+1的最大值

最长摆动序列定义成考虑到第i个数字(不一定以第i个数字结尾) 最后差为负的最大长度 以及最后差为正的最大程度两种情况

up[i]和down[i]

以up[i+1]的变化为例

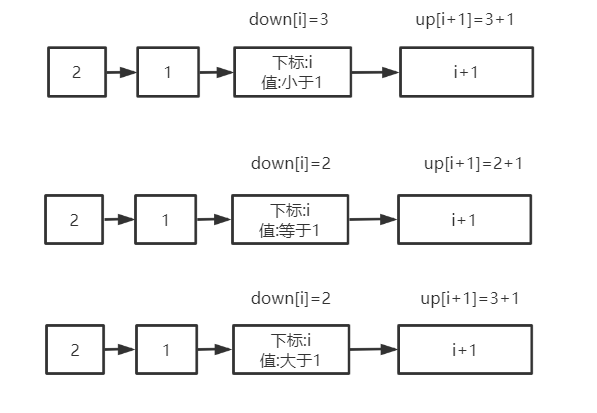
我们知道了arr[i+1]>arr[i]则up[i+1]=down[i]+1, 不论最后下降的两个数字在什么位置

​ arr[i+1]<=arr[i]则up[i+1]=up[i]不变

对于down也是这样

最后状态转移方程 $$ up[i+1]= \begin{cases} 1 & i=0 \
down[i]+1 & arr[i+1]>arr[i]且i>0 \
up[i] & arr[i+1]<=arr[i]且i>0 \end{cases} \————————-\
down[i+1]= \begin{cases} 1 & i=0 \
up[i]+1 & arr[i+1]<arr[i]且i>0 \
down[i] & arr[i+1]>=arr[i]且i>0 \end{cases} $$

参考leetcode题解https://leetcode-cn.com/problems/wiggle-subsequence/solution/tan-xin-si-lu-qing-xi-er-zheng-que-de-ti-jie-by-lg/

引用其例图方便理解

实现代码

func wiggleMaxLength(nums []int) int {
    length := len(nums)
    if(length<=0) {
        return 0
    }
    upDp, downDp := make([]int, length), make([]int, length)
    upDp[0], downDp[0] = 1, 1
    for i:=1; i< length; i++ {
        upDp[i] = upDp[i-1]
        downDp[i] = downDp[i-1]
        if nums[i] > nums[i-1] {
            upDp[i] = downDp[i-1]+1
        }else if nums[i] < nums[i-1] {
            downDp[i] = upDp[i-1]+1
        }
    }
    if upDp[length-1] > downDp[length-1] {
        downDp[length-1] = upDp[length-1]
    }
    return downDp[length-1]
    
}

1.为什么会用到动态规划呢？

一个长的摆动序列，逐个截取尾部的元素还是摆动序列

2.如何想到这种要考虑到两个状态转移的思路的呢？

整个题难点在于不是求最长连续的摆动序列而是允许删除部分元素

如果是连续的话和最长上升子序列完全是一个思路，但是如果是不连续的怎么做呢？

想法一：

知道一个范围内不连续的最长摆动序列， 我们如何推演出更大范围的最长摆动序列？

推不出来，因为更大范围多出来的一个元素和前一个元素的关系知道，但是也不知道 小范围 最后一个是上升还是下降呀

想法二： 既然不知道小范围是上升下降，那我们将问题状态细分，分成知道 一个范围内 结尾为上升态和下降态 最长摆动序列长度

如果小范围的摆动序列的最后两个数字包括arr[i]也可以吗通过比较arr[i+1]和arr[i]即可区分了，但是如果不包括呢？

想法三：即使不包括arr[i]也不影响？ 如果不包括arr[i],那上升态摆动序列最后的一个元素一定小于等于arr[i]

3.这道题如果用贪心算法如何求解呢？

每次上升尽可能上升到最大，每次下降尽可能下降到最小，这样维持一个贪心最优的摆动序列，一个一个挨个元素比较，o(n)时间即可解决

吐槽一下leet’code的计算耗时0ms,bug了。。。

474. 一和零

解题思路

题目和01背包问题类似，0-1背包问题如下:

给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

我们转换一下

给定一组物品，每种物品都有自己的重量（w[i]数组），在限定的总重量内，我们如何选择，才能拿到最多的物品。

dp[i][j]表示考虑前i件物品在容量为j的情况下可以拿到的最多物品数量,对于第i件物品有拿和不拿两种选择 $$ dp[i][j] = \begin{cases} dp[i-1][j] &j-w[i]<0装不下，只能不拿\
max(dp[i-1][j], dp[i-1][j-w[i]]+1) &j-w[i]>=0 装的下，拿或不拿 \end{cases} $$ 引申到我们现在的题目，背包容量变成了0和1的最大数量，其实就是重量变成了两个维度

dp[i][j][k]表示考虑前i件物品在容量为j,k的情况下可以拿到的最多物品数量，对于第i件物品有拿或不拿两种选择

$$ dp[i][j][k] = \begin{cases} dp[i-1][j][k] &j-arr0[i]<0||k-arr1[i]<0装不下，只能不拿\
max(dp[i-1][j][k], dp[i-1][j-arr0[i]][k-arr1[i]]+1) &j-arr0[i]>=0且k-arr1[i]>=0 装的下，拿或不拿 \end{cases} $$ arr0[i],arr1[i]表示第i个元素的 0和1的数量

实现代码

func findMaxForm(strs []string, m int, n int) int {
    strLen := len(strs)
    dp := make([][][]int, strLen+1)
    for i := 0; i < strLen+1; i++ {
        dp[i] = make([][]int, m+1)
        for j :=0; j < m+1; j++ {
            dp[i][j] = make([]int, n+1)
        }
    }
    for i:=1; i<=strLen;i++ {
        zeroCnt, oneCnt := zeroAndOneCount(strs[i-1])
        for j:=0;j<=m;j++ {
            for k:=0;k<=n;k++{
                if j>=zeroCnt&&k>=oneCnt {
                    dp[i][j][k] = Max(dp[i-1][j-zeroCnt][k-oneCnt]+1, dp[i-1][j][k])
                }else {
                    dp[i][j][k] = dp[i-1][j][k]
                }
            }
        }
    }
    return dp[strLen][m][n]
}

func zeroAndOneCount(s string) (int, int) {
    zero, one := 0, 0
    for _, ch := range s {
        if ch == '0' {
            zero++ 
        }else {
            one++
        }
    }
    return zero, one
}

func Max(a, b int) int {
    if a>b {
        b = a
    }
    return b
}